गति Motion

गति Motion

हम अपने चारों ओर की सृष्टि को देखकर पाते हैं कि कुछ वस्तुओं में समय के साथ-साथ उनकी स्थिति में परिवर्तन होता है, जबकि कुछ अपने स्थान पर ही स्थित रहती हैं, उदाहरणस्वरूप हमारे सामने से जाती रेलगाड़ी, मोटर आदि की स्थिति में समय के साथ परिवर्तन होता है, जबकि मेज पर पड़ी किताब आदि में परिवर्तन नहीं होता है। इससे पता चलता है कि हमारे चारों ओर स्थित वस्तुएँ या तो स्थित हैं या गतिमान हैं परन्तु वस्तु की यह स्थिरता अथवा गति हमारे सापेक्ष है, जैसे चलती रेलगाड़ी के डिब्बे में बैठा यात्री रेल पटरी की अपेक्षा गति में है, किन्तु डिब्बा के आपेक्षिक वह विराम है। अत: किन वस्तुओं की अपेक्षा कोई वस्तु गति में है, उन वस्तुओं को बताना जरूरी है परिभाषा से हम देखते हैं कि स्थिरता अथवा गति की अवस्थाओं का वर्णन सापेक्ष होता है।

गति के प्रकार  Type of Motion

1. सरलरेखीय गति Uniform Motion: जब एक वस्तु एक सीधी रेखा में गतिमान हो तो उसकी गति सरलरेखीय कहलाती है। उदाहरण-ढाल पर नीचे सरकता बालक, हाइवे पर चलती कार आदि।
2. वक्रीय गति Angular Motion: जब एक वस्तु किसी वक्रीय मार्ग के साथसाथ गतिमान हो, उसकी गति वक्रीय गति कहलाती है। उदाहरण-किसी वक्रीय सड़क पर मोड़ काटती गतिमान कार।
3. वृत्तीय गति Circular Motion: जब एक वस्तु किसी वृत्ताकार पथ पर इस तरह गतिमान हो कि उसकी गति किसी बिन्दु पर स्पर्श रेखा डालकर प्रदर्शित की जा सक जब उसकी गति वृत्ताकार कहलाती है। उदाहरण, सूर्य के चारों ओर पृथ्वी की गति, पृथ्वी के चारों ओर चंद्रमा की गति, परमाणु में नाभिक के चारों ओर इलेक्ट्रॉन की गति आदि।
4. कम्पनीय गति: जब कोई वस्तु किसी निश्चित बिन्दु के इधर-उधर गति करती है तो उसे कम्पनीय गति कहते हैं, जैसे-घड़ी के लोलक का अपनी मध्यमान स्थिति के दोनों ओर दोलन करना।

दूरी Distance

किसी दिये गये समयान्तराल में वस्तु द्वारा तय किये गये मार्ग की लम्बाई को दूरी कहते हैं। यह एक अदिश राशि है व सदैव धनात्मक होती है।

विस्थापन Displacement

किसी विशेष दिशा में गतिशील वस्तु के स्थित परिवर्तन को उसका विस्थापन कहते हैं। विस्थापन एक सदिश राशि है।

ज्ञातव्य है कि दूरी व विस्थापन में मुख्य अन्तर यह है कि वस्तु का विस्थापन धनात्मक, ऋणात्मक व शून्य कुछ भी हो सकता है, परन्तु दूरी सदैव धनात्मक होती है। जैसे हम किसी पत्थर को पृथ्वी से एक मीटर की ऊंचाई तक फेंकते हैं तथा पत्थर पुनः अपने स्थान पर वापस लौट आता है। इस दशा में पत्थर का विस्थापन तो शून्य होगा, परन्तु उसके द्वारा चली गयी कुल दूरी दो मीटर होगी।

वेग Velocity

गतिशील वस्तु के विस्थापन की दर अर्थात् एक सेकेण्ड में हुये विस्थापन को वस्तु का वेग कहते हैं।

वेग = विस्थापन / समय

वेग एक सदिश राशि है। इसका मात्रक मीटर/सेकण्ड होता है। वस्तु का वेग धनात्मक व ऋणात्मक दोनों हो सकता है।

चाल Speed

किसी गतिमान वस्तु को स्थिति परिवर्तन की दर अर्थात् एक सेकेण्ड में चली गई दूरी को उस वस्तु की चाल कहते हैं।

चाल = चली गई दूरी / समय

वस्तु की चाल एक अदिश राशि है व सदैव धनात्मक होती है। इसका मात्रक मी./से. होता है।

त्वरण Acceleration

यह आवश्यक नहीं है कि जो वस्तु गतिमान है, उसका वेग सदैव एक समान ही रहे। यह भी हो सकता है कि उसका वेग भिन्न-भिन्न समयों पर भिन्न-भिन्न रहे। यदि समय के साथ वस्तु का वेग बढ़ता या घटता है तो ऐसी गति को त्वरित गति कहते हैं तथा यह बताने के लिये कि वेग में किस दर से परिवर्तन होता है, हम एक नई राशि त्वरण का प्रयोग करते हैं। अत: “किसी गतिमान वस्तु के वेग में प्रति एकांक समयान्तराल में होने वाले परिवर्तन को उस वस्तु का त्वरण कहते है।’

त्वरण = वेग में परिवर्तन / समयान्तराल

त्वरण एक सदिश राशि है। यदि किसी वस्तु का वेग t₁ समय पर u₁ है तथा , t₂ समय पर u₂ है तो-

त्वरण = u₂ – u₁ /t₂– t₁

यदि समय के साथ वस्तु का वेग घटता है तो त्वरण ऋणात्मक होता है, जिसे मन्दन कहते हैं। M.K.S. पद्धति में इसका मात्रक मीटर/सेकण्ड² होता है।

नियत त्वरण वाली गति के समीकरण

यदि कोई वस्तु एक नियत त्वरण से एक ऋणु रेखा में चल रही हो तो उसके वेग, विस्थापन, समय तथा त्वरण के पारस्परिक सम्बन्धों को समीकरणों के द्वारा व्यक्त किया जा सकता है। यह समीकरण गति के समीकरण कहलाते हैं।

माना कि कोई वस्तु वेग u से चलना प्रारम्भ करती है तथा उसमें एक नियत त्वरण a है। माना कि t सेकण्ड में वस्तु s दूरी तय कर लेती है तथा उसका v वेग हो जाता है। तब u,a,t,s और v के सम्बन्धों को निम्न समीकरणों से व्यक्त किया जा सकता है –

V = u + at

S = ut + 1/2 at₂

तथा  V² = u² + 2as

यहाँ यह बात महत्वपूर्ण है कि ये समीकरण तभी लागू होता है जब त्वरण नियत हो तथा गति सरल रेखा में हो।

गति के नियम 

वस्तुओं की किसी आनत तल पर गति को देखकर गैलीलियों ने यह निष्कर्ष निकाला कि जब तक कोई बाह्य बल कार्य नहीं करता, वस्तुएँ एक निश्चित गति से चलती हैं। उन्होंने देखा कि काँच की गोली आनत तल पर लुढ़कती है तो उसका वेग बढ़ जाता है। गोली असंतुलित गुरुत्वीय बल के कारण नीचे गिरती है और नीचे पहुँचते-पहुँचते यह एक निश्चित वेग प्राप्त कर लेती है। जब यह काँच की गोली ऊपर की ओर चढ़ती है तब इसका वेग घटता है। दोनों ओर से एक आदर्श घर्षणरहित आनत तल पर एक गोली स्थिर है। गैलीलियो ने तक दिया कि जब गोली को बाईं ओर से छोड़ा जाता है तब यह ढाल पर नीचे की ओर लुढ़केगी तथा दाई ओर के आनत तल पर उतनी ही ऊँचाई तक जाएगी, जितनी ऊँचाई से उसे छोड़ा गया था। यदि दोनों ओर के तलों के झुकाव समान हैं तो गोली उतनी ही दूरी चढ़ेगी जितनी दूर तक कि वह लुढ़की थी। अगर दाई ओर के आनत तल के कोण को धीरे- धीरे कम किया जाए तो गोली को मूल ऊँचाई प्राप्त करने के लिए क्षैतिज तल पर लगातार चलती रहेगी। यहाँ गोली पर लगने वाला असंतुलित बल शून्य है। इस प्रकार यह ज्ञात होता है कि गोली की गति को बदलने के लिए एक असंतुलित बाह्य की आवश्यकता होती है लेकिन गोली की गति को एकरूप बनाए रखने के लिए किसी नेट बल की आवश्यकता नहीं होती है। वास्तविक अवस्था में शून्य असंतुलित बाह्य बल प्राप्त करना कठिन है। ऐसा गति की विपरीत दिशा में लगने वाले घर्षण बल के कारण होता है। इस प्रकार व्यवहार में गोली कुछ दूर चलने के बाद रुक जाती है। घर्षण के प्रभाव को न्यूनतम करने के लिए चिकनी काँच की गोली तथा चिकने समतल का प्रयोग एवं समतल की सतह पर चिकनाईयुक्त पदार्थ को लेप किया जाता है।

न्यूटन ने बल एवं गति के बारे में गैलीलियो के विचारों को आगे विकसित किया। उन्होंने तीन मौलिक नियमों को प्रस्तुत किया जो किसी वस्तु की गति को वर्णित करते हैं। इन नियमों को न्यूटन के गति के नियमों के नाम से जाना जाता है।

गति का प्रथम नियम First Law of Motion

प्रत्येक वस्तु अपनी स्थिर अवस्था या सरल रेखा के एक समान गति की अवस्था में बनी रहती है जब तक कि उस पर कोई बाहरी बल कार्यरत न हो।

दूसरे शब्दों में, सभी वस्तुएँ अपनी गति की अवस्था में परिवर्तन का विरोध करती हैं। गुणात्मक रूप में किसी वस्तु के विरामावस्था में रहने या एकसमान वेग के गतिशील रहने की प्रवृत्ति को जड़त्व कहते हैं। यही कारण है कि गति के पहले नियम को जड़त्व का नियम भी कहते हैं।

किसी मोटर गाड़ी में यात्रा करते समय होने वाले अनुभवों की व्याख्या जड़त्व के नियम द्वारा की जा सकती है। सीट के सापेक्ष हम तब तक विरामावस्था में रहते हैं जब तक कि मोटरगाड़ी को रोकने के लिए ब्रेक न लगाया जाए। ब्रेक लगाए जाने पर गाड़ी के साथ सीट भी विरामावस्था में आ जाती है, परंतु हमारा शरीर जड़त्व के कारण गतिज अवस्था में ही बने रहने की प्रवृत्ति रखता है। अचानक ब्रेक लगने पर सीट के आगे लगे पैनल से टकराकर हम घायल भी हो सकते हैं। इस तरह की दुर्घटनाओं से बचने के लिए सुरक्षा बेल्ट का उपयोग किया जाता है। ये सुरक्षा बेल्ट हमारे आगे बढ़ने की गति को धीमा करती है। इसके विपरीत अनुभव हमें तब होता है जब हम मोटर बस में खड़े होते हैं एवं मोटर बस अचानक चल पड़ती है। इस स्थिति में हम पीछे की ओर झुक जाते हैं। ऐसा इसलिए होता है, क्योंकि मोटर बस के अचानक गति में आ जाने से हमारा पैर, जो मोटर बस के फर्श के संपर्क में रहता है, गति में आ जाता है। परंतु शरीर का ऊपरी भाग जड़त्व के कारण इस गति का विरोध करता है।

जब कोई मोटरकार तीव्र गति के साथ किसी तीक्ष्ण मोड़ पर मुड़ती है तो हम एक ओर झुकने लगते हैं। इसे भी जड़त्व के नियम से समझा जा सकता है। हमारा शरीर अपनी एक सरल रेखीय गति को बनाए रखना चाहता है। जब मोटर कार की दिशा को बदलने के लिए इंजन द्वारा एक असंतुलित बल लगाया जाता है तब हम अपने शरीर के जड़त्व के कारण सीट पर एक ओर झुक जाते हैं।

जड़त्व तथा द्रव्यमान Inertia and Mass

प्रत्येक वस्तु अपनी गति की अवस्था में परिवर्तन का विरोध करती है। चाहे वह विरामावस्था में हो या गतिशील, वह अपनी मूल अवस्था को बनाए रखना चाहती है। वस्तु का यह गुण उसका जड़त्व कहलाता है। क्या सभी वस्तुओं का जड़त्व समान होता है? हम जानते हैं कि पुस्तकों से भरे बक्से को धक्का देने की अपेक्षा खाली बक्से को धक्का देना आसान होता है। उसी प्रकार हम एक फुटबॉल को किक लगाते हैं तो वह दूर चली जाती है जबकि अगर हम उतने ही बल से किसी उतने ही बड़े पत्थर पर किक लगाएँ, तो हो सकता है कि वह खिसके भी नहीं हो सकता है कि ऐसा करते समय हमें ही चोट लग जाए। एक ठेलागाड़ी को चलाने के लिए जितने बल की आवश्यकता होती है, उतना बल यदि किसी रेलगाड़ी पर लगाया जाए तो उसकी गति में न के बराबर परिवर्तन होगा। इस प्रकार हम कह सकते हैं कि रेलगाड़ी का जड़त्व ठेलागाड़ी से अधिक है। इससे स्पष्ट है कि भारी वस्तुओं का जड़त्व उसके द्रव्यमान से मापा जाता है। अत: हम जड़त्व और द्रव्यमान को निम्न रूप में परिभाषित कर सकते हैं –

किसी भी वस्तु का जड़त्व उसका वह प्राकृतिक गुण है, जो उसकी विराम या गति की अवस्था में परिवर्तन का विरोध करता है। इस प्रकार किसी वस्तु का द्रव्यमान उसके जड़त्व की माप है।

गति का द्वितीय नियम Second Law of Motion

गति का प्रथम नियम यह बताता है कि जब कोई असंतुलित बाह्य बल किसी वस्तु पर कार्य करता है तो उसके वेग में परिवर्तन होता है अर्थात् वस्तु त्वरण प्राप्त करती हैं अब हम देखेंगे कि किसी वस्तु का त्वरण उस पर लगाए गए बल पर कैसे निर्भर होता है तथा उस बल को हम कैसे मापते हैं। आइए कुछ दैनिक अनुभवों का अध्ययन करें। टेबल-टेनिस खेलने के दौरान यदि गेंद किसी खिलाड़ी के शरीर से टकराती है, तो वह घायल नहीं होता। गति से आती हुई क्रिकेट की गेंद किसी दर्शक को लगने के बाद उसको घायल कर सकती है। सड़क के किनारे खड़े किसी ट्रक

संवेग-संरक्षण के नियम Law of Conservation of Momentum

संरक्षण के समस्त नियमों; जैसे-संवेग, ऊर्जा, कोणीय संवेग, आवेश आदि के संरक्षण को भौतिकों में मौलिक नियम माना जाता है। ये सभी संरक्षण नियम प्रायोगिक प्रेक्षणों पर आधारित हैं। यह स्मरण रखना आवश्यक है कि संरक्षण के नियमों को प्रमाणित नहीं किया जा सकता। इन्हें प्रयोगों के द्वारा ही सत्यापित या खंडित किया जा सकता है। किसी भी संरक्षण नियम के अनुकूल प्रयोग के परिणाम उस नियम को सत्यापित तो करते हैं, लेकिन सिद्ध नहीं करते। दूसरी ओर, यदि एक भी प्रयोग के परिणाम इस नियम के विरुद्ध हों तो यह संरक्षण नियम को खंडित करने के लिए पर्याप्त होगा। संवेग संरक्षण का नियम विभिन्न प्रकार के निरीक्षणों एवं प्रयोगों के पश्चात् निगमित किया गया है। इस नियम को लगभग तीन शताब्दी पूर्व प्रतिपादित किया गया था। इस नियम को खंडित कर सकने वाली किसी स्थिति का अभी तक कोई अनुभव ज्ञात नहीं है। विभिन्न दैनिक अनुभवों को संवेग संरक्षण के नियम के आधार पर स्पष्ट किया जा सकता है।

से कोई दुर्घटना नहीं होती। परंतु 5 ms^-1 जैसी कम गति से चलते हुए ट्रक से टक्कर, रास्ते में खड़े किसी व्यक्ति की मृत्यु का कारण बन सकती है। एक छोटे द्रव्यमान की वस्तु जैसे गोली को अगर बंदूक से तीव्र वेग से छोड़ा जाए तो वह भी किसी व्यक्ति की मृत्यु का कारण बन सकती है। इससे पता चलता है कि वस्तु के द्वारा उत्पन्न प्रभाव वस्तु के द्रव्यमान एवं वेग पर निर्भर करता है। इसी प्रकार यदि किसी वस्तु को त्वरित किया जाता है, तो अधिक वेग प्राप्त करने के लिए अधिक बल की आवश्यकता होती है। दूसरे शब्दों में, हम कह सकते हैं कि वस्तु के द्रव्यमान एवं वेग से संबंधित एक महत्वपूर्ण राशि होती है। संवेग नामक इस राशि को न्यूटन ने प्रस्तुत किया था। किसी वस्तु का संवेग p उसके द्रव्यमान m  और वेग v के गुणनफल से परिभाषित किया जाता है।

p = mv

संवेग में परिमाण और दिशा दोनों होते हैं। इसकी दिशा वही होती है, जो वेग v की होती है। संवेग का SI  मात्रक किलोग्राम-मीटर/सेकंड होता है। चूंकि किसी असंतुलित बल के प्रयेाग से उस वस्तु के वेग में परिवर्तन होता है, इसलिए यह कहा जा सकता है कि बल ही संवेग को भी परिवर्तित करता है।

एक ऐसी अवस्था के बारे में विचार करें जिसमें खराब बैटरी वाली एक कार को सीधी सड़क पर 1 ms^-1 की गति प्रदान करने के लिए धक्का दिया जाता है, जो कि उसके इंजन को स्टार्ट करने के लिए पर्याप्त है। यदि एक या दो व्यक्ति इसे अचानक धक्का देते हैं तो भी यह स्टार्ट नहीं होती। लेकिन कुछ समय तक लगातार धक्का देने से कार उस गति को प्राप्त कर देती है। इससे स्पष्ट है कि कार के संवेग में परिवर्तन केवल बल के परिमाण से नहीं होता है, बल्कि उस समय से है जितने समय तक उस पर बल लगाया जाता है। इससे यह भी निष्कर्ष निकाला जा सकता है कि वस्तु के संवेग में परिवर्तन लाने में लगने वाला बल उसकी उस समय दर पर निर्भर करता है, जिसमें कि संवेग में परिवर्तन होता है।

गति का द्वितीय नियम यह बताता है कि किसी वस्तु के संवेग में परिवर्तन की दर उस पर लगने वाली असंतुलित बल की दिशा में समय समानुपातिक होती है।

F = Р₂ –Р₁ / t₂ – t₁

गति का तृतीय नियम Third Law of Motion

पहले दोनों गति के नियमों से हमें ज्ञात होता है कि कोई प्रयुक्त बल वस्तु की गति की अवस्था में परिवर्तन लाता है तथा इनमें हमें बल को मापने की विधि भी प्राप्त होती है। गति के तीसरे नियम के अनुसार, जब एक वस्तु पर दूसरी वस्तु द्वारा तात्क्षणिक बल लगाया जाता है, ये दोनों बल परिमाण में सदैव समान लेकिन दिशा में विपरीत होते हैं। ये बल कभी एक ही वस्तु पर कार्य नहीं करते हैं। फुटबॉल के खेल में प्राय: हम गेंद को तेज गति से किक मारने के क्रम में विपक्षी टीम के खिलाड़ी से टकरा जाते हैं। इस क्रम में दोनों खिलाड़ी एक-दूसरे पर बल लगाते हैं, अतएव दोनों ही खिलाड़ी चोटिल होते हैं। दूसरे शब्दों में, किसी एकल बल का अस्तित्व नहीं होता बल्कि ये सदैव युगल रूप में होते हैं। इन दोनों विरोधी बलों को क्रिया तथा प्रतिक्रिया बल कहा जाता है।

माना कि दो स्प्रिंग तुलाएँ एक-दूसरे से जुडी हैं, तुला B का स्थिर सिरा दीवार से जुड़ा है। जब तुला A के मुक्त सिरे पर बल लगाया जाता है तब हम पाते हैं कि दोनों तुलाएँ एक ही मान दर्शाती हैं। अर्थात् तुलना A द्वारा तुला B पर प्रयुक्त बल तुला B के द्वारा तुला A पर लगाए गए बल के परिमाण में समान है परंतु इन दोनों बलों की दिशाएँ परस्पर विपरीत हैं। तुला A के द्वारा तुला B पर लगाया गया बल प्रतिक्रिया है। अत: गति के तृतीय नियम को इस प्रकार भी व्यक्त किया जाता है: किसी भी क्रिया के लिए ठीक उसके समान कितु विपरीत दिशा में प्रतिक्रिया होती है। यद्यपि यह अवश्य याद रखना चाहिए कि क्रिया और प्रतिक्रिया बल सदैव दो अलग-अलग वस्तुओं पर कार्य करते हैं।

माना कि आप विश्राम की अवस्था में हैं और सड़क पर चलना प्रारंभ करते हैं। द्वितीय नियम के अनुसार इसके लिए एक बल की आवश्यकता होती है, जो आपके शरीर में त्वरण उत्पन्न करता हैं यह कौन-सा बल है? क्या यह पेशीय बल है, जो आप सड़क पर लगाते हैं? क्या यह बल हम उसी दिशा में लगाते हैं, जिस दिशा में हम आगे बढ़ते हैं? नहीं, हम सड़क के पृष्ठ को अपने पैरों से पीछे धकेलते हैं। सड़क भी आपके पैर पर उतना ही प्रतिक्रिया बल विपरीत दिशा में लगाती है जिसके प्रभाव से आप आगे बढ़ते हैं।

यह जानना आवश्यक है कि यद्यपि क्रिया और प्रतिक्रिया बल परिमाण में हमेशा समान होते हैं फिर भी ये बल एक समान परिमाण के त्वरण उत्पन्न नहीं कर सकते। ऐसा इसलिए है क्योंकि प्रत्येक बल अलग-अलग द्रव्यमान की वस्तुओं पर कार्य करता है।

बंदूक से गोली छोड़ने की अवस्था में, बंदूक द्वारा गोली पर आगे की ओर एक बल आरोपित होता है। गोली भी बंदूक पर एक समान परंतु विपरीत दिशा में प्रतिक्रिया बल लगाती है। इससे बंदूक पीछे की ओर प्रतिक्षेपित होती है। चूंकि बंदूक का द्रव्यमान गोली के द्रव्यमान से अधिक होता है। अत: बंदूक का त्वरण गोली के त्वरण से काफी कम होता है। एक नाविक द्वारा नाव से आगे की ओर कूदने की स्थिति में भी, गति के तीसरे नियम को प्रदर्शित किया जा सकता है। नाविक आगे की ओर कूदता है तो नाव पर लगने वाला प्रतिक्रिया बल नाव को पीछे की ओर धकेलता है।

गुरूत्वीय गति के समीकरण

पृथ्वी वस्तु को अपने केन्द्र की ओर खींचती है। इस खिंचाव के कारण पृथ्वी की ओर, स्वतंत्रतापूर्वक गिरती हुई वस्तु में एक नियम त्वरण उत्पन्न हो जाता है। इसे गुरूत्वीय त्वरण कहते हैं तथा g से प्रदर्शित करते हैं। इसका मान लगभग 9.8 मीटर/सेकेण्ड² होता है या 32.2 फीट सेकेण्ड² है (अथवा पृथ्वी से ऊपर फेंकी गई) वस्तुओं की गति को गुरूत्वीय गति कहते हैं। यदि हम गति के तीनों समीकरणों में d के स्थान पर g रख दे तथा S (दूरी) के स्थान पर h ऊंचाई रख दें तो पृथ्वी की ओर गिरती हुई वस्तुओं के लिए समीकरण आ जायेंगे।

अर्थात्

(i) V = u + gt

(ii) h = ut + 1/2 gt²

(iii) V² = u² + 2gh

यदि वस्तु किसी ऊंचाई से मुक्त रूप से छोड़ी गई है तो वस्तु का प्रारम्भिक वेग u = o होगा।

गुरूत्वीय तत्वरण g की दिशा केन्द्र पृथ्वी के केन्द्र की ओर होती है अत: जब हम किसी वस्तु को पृथ्वी से ऊपर की ओर फेंकते हैं तो इसमें गुरूत्वीय मंदन उत्पन्न होता है, जिसके कारण इसका वेग लगातार घटता है तथा कुछ ऊंचाई पर पहुंचने के बाद ही वस्तु गुरूत्वाकर्षण के कारण नीचे चलने लगती है और गुरूत्वीय त्वरण के कारण बढ़ते हुये वेग से पृथ्वी पर आ जाती है। पृथ्वी से ऊपर की ओर जाती हुई वस्तु की गति के समीकरण प्राप्त करने के लए हम गति के समीकरणों में g के स्थान पर –g रखेंगे।

(i) V = u – gt

(ii) h = ut — 1/2 gt²

(iii) V²= u²– 2gh

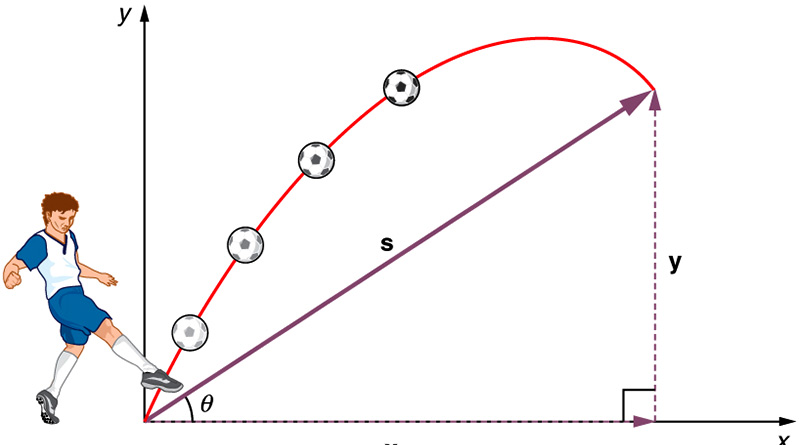
प्रक्षेप्य गति Projectile Motion

जब कोई वस्तु क्षैतिज से कोई कोण बनाते हुए उर्ध्वाधर तल में प्रक्षेपित की जाती है तो उसका पथ परवलय होता है। पिण्ड की यह गति प्रक्षेप्य गति कहलाती है। यह समान वेग से क्षैतिज गति तथा समान त्वरण से उर्ध्वाधर गति का परिणाम है।

उड्डयन काल Time of Flight

पिण्ड को फेंकने तथा उसके वापस पृथ्वी पर गिरने तक के बीच के समय को उड्डयन काल कहते हैं।

परास Range

पिण्ड अपने उड्डयन काल में जितनी क्षैजित दूरी तय करता है, उसे परास कहते हैं।

एकसमान वृत्तीय गति Uniform Circular Motion

एक वृत्तीय पथ के साथ-साथ किसी पिण्ड की गति वृत्तीय गति कहलाती है। वृतीय गति के दौरान, किसी निश्चित बिन्दु पर गति की दिशा को उस बिन्दु पर स्पर्श रेखा डालकर जाना जाता है। उदाहरण

1. पृथ्वी तथा अन्य ग्रह सूर्य को इर्द-गिर्द वृत्तीय पथ पर चक्कर काटते हैं।
2. चन्द्रमा भी पृथ्वी के इर्द-गिर्द वृत्तीय पथ पर गतिशील है।
3. एक मजबूत धागे से बंधा पत्थर जब घुमाया/हिलाया जाता है, तो वह पत्थर की वृत्तीय गति को संकेतित करता है।

वृत्ताकार पथ पर चलने के लिए वस्तु को अपनी दिशा प्रत्येक बिंदु पर बदलनी पड़ेगी। अतः वृत्त में एक समान चाल से चल रही वस्तु की चाल में कोई परिवर्तन नहीं होता, किंतु वस्तु की गति की दिशा लगातार बदलती रहती है। अथात्, एक समान वृत्तीय गति में वेग का परिमाण अचर रहता है और वेग की दिशा हर बिंदु पर स्पर्श रेखा की दिशा में होती है। अतएव एकसमान चाल में एकसमान वेग अंतनिर्हित नहीं है।

कोणीय वेग को समय के सापेक्ष कोणीय विस्थापन के परिवर्तन की दर के रूप में परिभाषित किया जाता है। कोणीय वेग को ग्रीक अक्षर ω से प्रदर्शित किया जाता है।

इस प्रकार

वेग ω = कोणीय विस्थापन / समय = θ / t  रेडियन

कोणीय विस्थापन: गतिशील वस्तु को वृत्त के केन्द्र से जोड़ने वाली रेखा द्वारा कोण कोणीय विस्थापन कहलाता है। कोणीय विस्थापन को रेडियन मात्रकों में मापा जाता है।

कोणीय त्वरण: कोणीय वेग को परिवर्तन की दर को कोणीय त्वरण कहते हैं।

कोणीय त्वरण का मात्रक रेडियन/सेकण्ड² है। तथा विमीय सूत्र T² है।

अभिकेन्द्र त्वरण Centripetal Acceleration

जब कोई कण एकसमान वृत्तीय गति करता है तो कण की चाल अचर होते हुए भी उसकी दिशा लगातार बदलती रहती है अर्थात् उसका वेग निरन्तर बदलता रहता है। अत: वृत्तीय गति में त्वरण रहता है। इस त्वरण की दिशा सदैव उस वृत्त के केन्द्र की ओर रहती है। अत: इसे अभिकेन्द्र त्वरण कहते हैं।

जहाँ a, उस कण का अभिकद्रीय त्वरण, r वृत्त की त्रिज्या, v रेखीय वेग तथा कोणीय वेग है।

a = v²/ अथवा a = rω²

अभिकेन्द्रीय तथा अपकेन्द्रीय बल Central and Centrifugal Force

जब कोई पिण्ड किसी वृत्तीय मार्ग पर चलता है, तो उस पर मार्ग के केन्द्र की ओर एक बल लगता है, जिसे अभिकेन्द्रीय बल कहते हैं। अत: जहाँ F बल, m वृत्तीय गति करती हुई वस्तु का द्रव्यमान, v वेग तथा r त्रिज्या है।

न्यूटन के तीसरे नियम के अनुसार इस बल का एक प्रतिक्रिया बल, जो कि परिमाण में अभिकेन्द्रीय बल के बराबर परन्तु इसकी दिशा अभिकेन्द्रीय बल के विपरीत अर्थात् केन्द्र से बाहर की ओर होती है, लगता है। इस प्रतिक्रिया बल को ही अपकेन्द्रीय बल कहते हैं। सर्कस में मौत के कुयें के खेल में मोटर साईकिल सवार पर दीवार द्वारा अभिकेन्द्रीय बल अन्दर की ओर लगाया जाता है, जबकि इसकी प्रतिक्रिया बल सवार द्वारा दीवार पर बाहर की ओर दीवार पर लगाया जाता है। कपड़ा सुखाने की मशीन, दूध से मक्खन निकालने की मशीन आदि आपकेन्द्रीय बल के सिद्धान्त पर कार्य करती हैं।